递归算法示例
布朗桥
public class Brownian {
// midpoint displacement method
public static void curve(double x0, double y0, double x1, double y1, double var, double s) {
// stop if interval is sufficiently small
if (Math.abs(x1 - x0) < 0.01) {
StdDraw.line(x0, y0, x1, y1);
return;
}
double xm = (x0 + x1) / 2;
double ym = (y0 + y1) / 2;
ym = ym + StdRandom.gaussian(0, Math.sqrt(var));
curve(x0, y0, xm, ym, var/s, s);
curve(xm, ym, x1, y1, var/s, s);
}
public static void main(String[] args) {
double hurstExponent = Double.parseDouble(args[0]);
double s = Math.pow(2, 2*hurstExponent);
curve(0.0, 0.5, 1.0, 0.5, 0.01, s);
}
} 布朗桥生成一个函数图,它近似于分数布朗运动的一个简单例子,即布朗桥。你可以把这个图看作是连接两点(x0,y0)和(x1,y1)的随机游动,由几个参数控制。该实现基于中点位移法,这是在x-区间[x0,x1]内绘制曲线的递归方案。基本情况(当间隔的大小小于给定公差时)是绘制一条连接两个端点的直线。缩减情况是将间隔分成两半,步骤如下:
曲线的形状由两个参数控制:波动率(方差的初始值)控制图形偏离连接点的直线的距离,Hurst指数控制曲线的平滑度。

递归的陷阱
使用递归,您可以编写紧凑而优雅的程序,这些程序在运行时会出现惊人的失败。
1.缺少基本情况:
public class NoBaseCase {
public static double harmonic(int n) {
return harmonic(n-1) + 1.0/n;
}
public static void main(String[] args) {
int n = Integer.parseInt(args[0]);
StdOut.println(harmonic(n));
}
}如果调用此函数,它将重复调用自己,并且永远不会返回。
2.不能保证趋同
另一个常见的问题是在递归函数中包含一个递归调用来解决不小于原始问题的子问题。例如下面的代码对于其参数的任何值(1除外)进入无限递归循环。
public class NoConvergence {
public static double harmonic(int n) {
if (n == 1) return 1.0;
return harmonic(n) + 1.0/n;
}
public static void main(String[] args) {
int n = Integer.parseInt(args[0]);
StdOut.println(harmonic(n));
}
}
3.内存需求过大
如果函数在返回之前递归调用自身的次数过多,则Java跟踪递归调用所需的内存可能会被禁止。下面的代码计算第n次谐波数。但是,用一个巨大的n值调用它将导致stackoverflower。
public class ExcessiveMemory {
public static double harmonic(int n) {
if (n == 1) return 1.0;
return harmonic(n-1) + 1.0/n;
}
public static void main(String[] args) {
int n = Integer.parseInt(args[0]);
StdOut.println(harmonic(n));
}
}
4.过度的重新计算
计算Fibonacci数的错误方法编写一个简单的递归程序来解决一个问题的疑惑,必须始终通过这样一种理解来缓和:由于过度的重新计算,一个简单的程序可能需要指数时间(不必要的)。例如,Fibonacci序列
0,1,1,2,3,5,8,13,21,34,55,89,144,233。。。由公式定义:
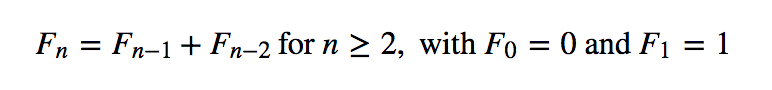
public class Fibonacci {
public static long fibonacci(int n) {
if (n <= 1) return n;
else return fibonacci(n-1) + fibonacci(n-2);
}
public static void main(String[] args) {
int n = Integer.parseInt(args[0]);
for (int i = 1; i <= n; i++)
StdOut.println(i + ": " + fibonacci(i));
}
}然而,这个程序是惊人的低效!为了了解为什么这样做是徒劳的,考虑一下函数是如何计算fibonacci(8)=21。它首先计算fibonacci(7)=13和fibonacci(6)=8。为了计算fibonacci(7),它再次递归地计算fibonacci(6)=8,fibonacci(5)=5。情况迅速恶化。当计算fibonacci(n)精确为Fn时,此程序计算fibonacci(1)的次数。
动态规划
动态规划是实现递归程序的一种通用方法,其基本思想是将一个复杂问题递归地划分为若干较简单的子问题;存储每个子问题的答案;并最终使用存储的答案来解决原始问题。通过只解决每个子问题一次(而不是一次又一次),这种技术避免了运行时间内潜在的指数爆炸。
自顶向下的动态规划。在自顶向下的动态编程中,我们存储或缓存我们解决的每个子问题的结果,以便下次需要解决相同的子问题时,我们可以使用缓存的值,而不是从头开始解决子问题。下面的代码说明了计算Fibonacci数的自顶向下动态规划。
public class TopDownFibonacci {
private static long[] f = new long[92];
public static long fibonacci(int n) {
if (n == 0) return 0;
if (n == 1) return 1;
// return cached value (if previously computed)
if (f[n] > 0) return f[n];
// compute and cache value
f[n] = fibonacci(n-1) + fibonacci(n-2);
return f[n];
}
public static void main(String[] args) {
int n = Integer.parseInt(args[0]);
for (int i = 1; i <= n; i++)
StdOut.println(i + ": " + fibonacci(i));
}
}
1.自下而上的动态规划
在自下而上的动态规划中,我们计算所有子问题的解,从“最简单”的子问题开始,逐步建立越来越复杂的子问题的解决方案。下面的代码说明了计算Fibonacci数的自底向上动态规划。
public class BottomUpFibonacci {
public static long fibonacci(int n) {
long[] f = new long[n+1];
f[0] = 0;
f[1] = 1;
for (int i = 2; i <= n; i++)
f[i] = f[i-1] + f[i-2];
return f[n];
}
public static void main(String[] args) {
int n = Integer.parseInt(args[0]);
for (int i = 1; i <= n; i++)
StdOut.println(i + ": " + fibonacci(i));
}
}这个视频演示了递归算法:
2.最长公共子序列问题
给定两个字符串x和y,我们希望计算它们的(LCS)。如果我们从x中删除一些字符,从y中删除一些字符,而得到的两个字符串相等,则我们将结果字符串称为公共子序列。LCS的问题是找到两个字符串的一个尽可能长的公共子序列。例如,ggcacag和ACGGCGGATACG的LCS是GGCAACG,一个长度为7的字符串。
- - G G C - - A - C C A C G
A C G G C G G A T - - A C G3.最长公共子序列递归
现在我们描述一个递归公式,它使我们能够找到两个给定字符串s和t的LCS。设m和n分别是s和t的长度。我们用符号s[i..m)表示从索引i开始的s的后缀,而t[j..n)表示从索引j开始的t的后缀。
如果s和t以相同的字符开头,则s和t的LCS包含第一个字符。因此,我们的问题归结为寻找后缀s[1..m)和t[1..n]的LCS。
如果s和t以不同的字符开头,则这两个字符不能是公共子序列的一部分,因此可以安全地丢弃其中一个。在这两种情况下,问题都归结为找到两个字符串的LCS:s[0..m)和t[1..n)或s[1..m)和t[0..n]。
一般来说,如果我们让opt[i][j]表示后缀s[i..m)和t[j..n]的LCS的长度,则以下递归成立:
opt[i][j] = 0 if i = m or j = n
= opt[i+1][j+1] + 1 if s[i] = t[j]
= max(opt[i][j+1], opt[i+1][j]) otherwise4.动态规划解决方案
下面的代码从一个自下而上的动态规划方法开始解决这个问题:
public class LongestCommonSubsequence {
// Compute length of LCS for all subproblems.
public static String lcs(String x, String y) {
int m = x.length(), n = y.length();
int[][] opt = new int[m+1][n+1];
for (int i = m-1; i >= 0; i--) {
for (int j = n-1; j >= 0; j--) {
if (x.charAt(i) == y.charAt(j)) {
opt[i][j] = opt[i+1][j+1] + 1;
}
else {
opt[i][j] = Math.max(opt[i+1][j], opt[i][j+1]);
}
}
}
// Recover LCS itself.
String lcs = "";
int i = 0, j = 0;
while (i < m && j < n) {
if (x.charAt(i) == y.charAt(j)) {
lcs += x.charAt(i);
i++;
j++;
}
else if (opt[i+1][j] >= opt[i][j+1]) i++;
else j++;
}
return lcs;
}
public static void main(String[] args) {
String lcs = lcs(args[0], args[1]);
StdOut.println(lcs);
}
}

最后一个挑战是恢复最长的公共子序列本身,而不仅仅是它的长度。其关键思想是将动态规划算法的步骤向后追溯,重新发现选项(在图中以灰色突出显示)从opt[0][0]到opt[m][n]的路径。为了确定导致选择[i][j]的选择,我们考虑三种可能性:
- 字符
s[i]与t[j]匹配。在这种情况下,必须有opt[i][j]=opt[i+1][j+1]+1,并且LCS中的下一个字符是s[i]。我们继续从opt[i+1][j+1]追溯 - LCS不包含
s[i]。在本例中,opt[i][j]=opt[i+1][j],我们继续从opt[i+1][j]追溯 - LCS不包含
t[j]。在本例中,opt[i][j]=opt[i][j+1],我们继续从opt[i][j+1]追溯
其他问题可以参考这篇文章介绍:https://javakk.com/584.html
