Java中的递归
什么是递归?
函数直接或间接调用自身的过程称为递归,相应的函数称为递归函数。使用递归算法,某些问题可以很容易地解决。这类问题的例子有Hanoi的Towers(TOH)、序/前序/后序树遍历、图的DFS等。
递归中的基本条件是什么?
在递归程序中,给出了基本情况的解,大问题的解用小问题表示。
int fact(int n)
{
if (n < = 1) // base case
return 1;
else
return n*fact(n-1);
}在上面的例子中,定义了n<=1的基本情况,并且可以通过转换为较小的数值来求解较大的数值,直到达到基本情况为止。
如何使用递归来解决特定问题?
其思想是用一个或多个较小的问题来表示问题,并添加一个或多个停止递归的基本条件。例如,如果我们知道(n-1)的阶乘,我们就计算阶乘n。对于基数为0的情况。当n=0时返回1。
递归中为什么会出现堆栈溢出错误?
如果未定义堆栈,则可能出现溢出。让我们举个例子来理解这一点。
int fact(int n)
{
// wrong base case (it may cause
// stack overflow).
if (n == 100)
return 1;
else
return n*fact(n-1);
}如果调用fact(10),它将调用fact(9)、fact(8)、fact(7),依此类推,但数字永远不会达到100。所以,基本情况没有达到。如果堆栈上的这些函数耗尽了内存,则会导致堆栈溢出错误。
直接递归和间接递归有什么区别?
如果函数fun调用相同的函数fun,则称为直接递归函数。如果函数fun调用另一个函数say fun_new,而fun_new直接或间接调用fun,则称为间接递归函数。表1说明了直接递归和间接递归之间的区别。
直接递归:
void directRecFun()
{
// Some code....
directRecFun();
// Some code...
}间接递归:
void indirectRecFun1()
{
// Some code...
indirectRecFun2();
// Some code...
}
void indirectRecFun2()
{
// Some code...
indirectRecFun1();
// Some code...
}有尾递归和无尾递归有什么区别?
当递归调用是函数执行的最后一件事时,递归函数是尾部递归的。
如何在递归中为不同的函数调用分配内存?
从main() 调用任何函数时,内存都会在堆栈上分配给它。递归函数调用自己,被调用函数的内存被分配到调用函数的内存之上,并且为每个函数调用创建不同的局部变量副本。当达到基本情况时,函数将其值返回给调用它的函数,内存被取消分配,进程继续。
让我们以一个简单函数为例说明递归是如何工作的。
// A Java program to demonstrate
// working of recursion
class GFG {
static void printFun(int test)
{
if (test < 1)
return;
else {
System.out.printf("%d ", test);
// Statement 2
printFun(test - 1);
System.out.printf("%d ", test);
return;
}
}
public static void main(String[] args)
{
int test = 3;
printFun(test);
}
} 输出:
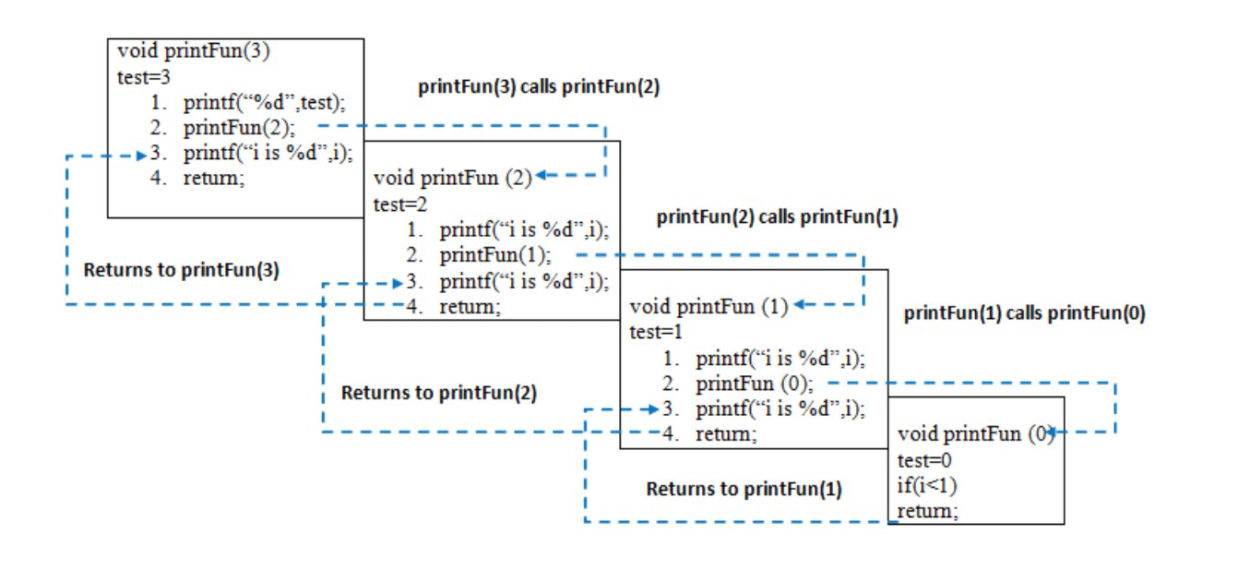
3 2 1 1 2 3从 main() 调用printFun(3)时,内存分配给printFun(3),局部变量测试初始化为3,语句1到4被推送到堆栈上,如下图所示。它首先打印“3”。在语句2中,调用printFun(2),并将内存分配给printFun(2),局部变量测试初始化为2,语句1到4被推送到堆栈中。类似地,printFun(2)调用printFun(1),printFun(1)调用printFun(0)。printFun(0)转到if语句并返回到printFun(1)。执行printFun(1)的其余语句并返回printFun(2),依此类推。在输出中,打印3到1的值,然后打印1到3。内存堆栈如下图所示。
递归编程相对于迭代编程有什么缺点?
注意递归程序和迭代程序具有相同的问题解决能力,即每个递归程序都可以迭代编写,反之亦然。递归程序比迭代程序有更大的空间需求,因为在达到基本情况之前,所有函数都将保留在堆栈中。由于函数调用和返回开销,它还需要更大的时间。
递归编程与迭代编程相比有什么优点?
递归为编写代码提供了一种简洁的方法。有些问题本质上是递归的,如树遍历、河内塔等。对于这些问题,最好编写递归代码。我们也可以用这样的代码结构来迭代地编写数据栈。例如参考有序树遍历无递归,迭代塔河内。
在Java中,函数调用机制支持方法本身调用的可能性。这种功能称为递归。
例如,假设我们要将0到某个值n的整数求和:
public int sum(int n) {
if (n >= 1) {
return sum(n - 1) + n;
}
return n;
}递归函数有两个主要要求:
停止条件–函数在满足某个条件时返回一个值,而无需进一步的递归调用
递归调用–函数用一个更接近停止条件的输入调用自身
每次递归调用都会向JVM的堆栈内存添加一个新帧。因此,如果我们不注意递归调用的深度,可能会发生内存不足异常。
利用尾部递归优化可以避免这个潜在的问题。
尾递归与头递归
当递归调用是函数执行的最后一件事时,我们将递归函数称为尾部递归。否则,称为头递归。
上面sum()函数的实现是头递归的一个例子,可以改为尾递归:
public int tailSum(int currentSum, int n) {
if (n <= 1) {
return currentSum + n;
}
return tailSum(currentSum + n, n - 1);
}
对于尾部递归,递归调用是该方法所做的最后一件事,因此在当前函数中没有任何东西可以执行。
因此,逻辑上不需要存储当前函数的堆栈帧。
尽管编译器可以利用这一点来优化内存,但应该注意的是,Java编译器目前还没有针对尾部递归进行优化。
递归与迭代
递归可以帮助简化一些复杂问题的实现,使代码更清晰、更具可读性。
但是正如我们已经看到的,递归方法通常需要更多的内存,因为每次递归调用所需的堆栈内存都会增加。
作为一种选择,如果我们可以用递归来解决问题,我们也可以通过迭代来解决它。
例如,我们的sum方法可以通过迭代实现:
public int iterativeSum(int n) {
int sum = 0;
if(n < 0) {
return -1;
}
for(int i=0; i<=n; i++) {
sum += i;
}
return sum;
}
在迭代方法中,递归可以潜在地给出更好的性能。也就是说,与递归相比,迭代将更复杂,更难理解,例如:遍历二叉树。
在头递归、尾递归和迭代方法之间做出正确的选择都取决于具体的问题和情况。
递归代码示例
求十的N次方
假设我们需要计算10的n次方。这里我们的输入是n。用递归的方法,我们可以先计算10的(n-1)次方,然后将结果乘以10。
然后,计算10的(n-1)次方将是10的(n-2)次方,并将结果乘以10,依此类推。我们继续这样,直到我们需要计算10的(n-n)次方,即1。
如果我们想在Java中实现这一点,我们可以写下:
public int powerOf10(int n) {
if (n == 0) {
return 1;
}
return powerOf10(n-1) * 10;
}Fibonacci数列第N个元素的求法
从0和1开始,Fibonacci序列是一个数字序列,其中每个数字被定义为两个数字的总和:0 1 1 1 2 3 5 8 13 21 34 55…
所以,给定一个数n,我们的问题是找到Fibonacci序列的第n个元素。要实现递归解决方案,我们需要找出停止条件和递归调用。
幸运的是,这真的很简单。
我们把f(n)称为序列的第n个值。然后我们将得到f(n)=f(n-1)+f(n-2)(递归调用)。
同时,f(0)=0,f(1)=1(停止条件)。
那么,我们很明显可以定义一个递归方法来解决问题:
public int fibonacci(int n) {
if (n <= 1) {
return n;
}
return fibonacci(n-1) + fibonacci(n-2);
}从十进制到二进制的转换
现在,让我们考虑一下将十进制数转换为二进制数的问题。要求是实现一个方法,该方法接收一个正整数值n并返回一个二进制字符串表示。
将十进制数转换为二进制的一种方法是将值除以2,记录余数并继续将商除以2。
我们一直这样除法,直到得到0的商。然后,通过按保留顺序写出所有余数,得到二进制字符串。
因此,我们的问题是编写一个按保留顺序返回这些余数的方法:
public String toBinary(int n) {
if (n <= 1 ) {
return String.valueOf(n);
}
return toBinary(n / 2) + String.valueOf(n % 2);
}二叉树的高度
二叉树的高度定义为从根到最深叶的边数。我们现在的问题是计算给定二叉树的这个值。
一个简单的方法是找到最深的叶子,然后计算根和叶子之间的边缘。
但是考虑递归的解决方案,我们可以将二叉树的高度定义为根的左分支和根的右分支的最大高度加1。
如果根没有左分支和右分支,则其高度为零。
以下是我们的实现:
public int calculateTreeHeight(BinaryNode root){
if (root!= null) {
if (root.getLeft() != null || root.getRight() != null) {
return 1 +
max(calculateTreeHeight(root.left),
calculateTreeHeight(root.right));
}
}
return 0;
}因此,我们看到有些问题可以用递归以一种非常简单的方式来解决。
